Plenarvorträge 1990

Vortrag am 14.12.1990
Egon Fanghänel (Halle-Wittenberg), Ordentliches Mitglied der Mathematisch-naturwissenschaftlichen Klasse:

„Vom Seifensieden zur Mizellkatalyse“

Obwohl die Herstellung von Seife durch alkalische Hydrolyse von Fetten und Ölen bereits v. Chr. bekannt war, beginnt die eigentliche Tensidchemie erst in unserem Jahrhundert. In den zwanziger und dreißiger Jahren wurde mit der Hydrierung von Fetten zu Fettalkoholen die Herstellung weiterer Tenside möglich. Seit den fünfziger Jahren werden Tenside auch auf petro1chemischer Basis hergestellt. Heute ist eine Vielzahl von Tensiden bekannt und auf dem Markt, wobei die einzelnen Produkte entsprechend ihren Eigenschaften in verschiedenen Fertigerzeugnissen enthalten sind oder als Hilfsstoffe bei industriellen Prozessen Anwendung finden. Neben der stürmischen Entwicklung der Tensidherstellung und -anwendung vollzog sich in unserem Jahrhundert ein intensives Studium der physikalisch-chemischen Eigenschaften der Tenside. Eine dieser Eigenschaften ist die Fähigkeit der Tensidmoleküle, in wäßrigen Lösungen oberhalb der kritischen Mizellkonzentration zu Mizellen und anderen Aggregaten zu assoziieren.

Mizellen sind in der Lage, Moleküle organischer Verbindungen und im Vergleich zum Tensid entgegengesetzt geladene Ionen zu solubilisieren. Damit können chemische Re­aktionen zwischen im Bereich von Mizellen solubilisierten Reaktionspartnern durch­geführt werden. Der Einfluß von Mizellen auf Photoreaktionen kann genutzt werden, um Informationen über die Struktur und die Eigenschaften der Mizellen zu erhalten. Anhand von Beispielen wird gezeigt, wie die Polarität und die Viskosität in der Sternregion sowie das Oberflächenpotential und die mittlere Aggregationszahl der Mizellen mit photochemischen Methoden bestimmt werden können. Der Mizelleinfluß auf photo­chemische und thermische Reaktionen kann andererseits genutzt werden, um diese Reaktionen gezielt in ihrer Geschwindigkeit (Mizellkatalyse) oder in Richtung der Produkt­bildung zu beeinflussen. Die Untersuchung von chemischen Reaktionen in mizellaren Lösungen ist damit ein Beispiel für das fruchtbare Zusammenwirken von Tensidchemie, Photochemie und chemischer Kinetik.

 

Vortrag am 14.12.1990
Ulrich Ricken (Halle-Wittenberg), Ordentliches Mitglied der Philologisch-historischen Klasse:

„Wie wurde »Idee« ein deutsches Wort? Zur Begriffsgeschichte der deutschen Aufklärung im europäischen Kontext“

Erst während des 18. Jahrhunderts wurde das Wort Idee in die deutsche Sprache eingebürgert, im Verlauf eines Prozesses, der sich mit wichtigen Etappen der deutschen Aufklärung und ihren Wechselbeziehungen im europäischen Kontext verbindet.

Der Vortrag gliedert sich in zwei Teile:

1. Idee oder Begriff?
   Christian Wolff und die Ausbildung einer deutschen philosophischen Terminologie und Wissenschaftssprache
2. Begriff und Idee.
   Eine neue Etappe der deutschen Aufklärung und ihrer Terminologie

Das lateinische Wort idea war Bestandteil eines wichtigen Begriffsfeldes der europäischen Kulturgeschichte, nachdem sein griechisches Etymon schon vor Plato im Mittelpunkt philosophischer Reflexion stand. Den Auftakt für die zentrale Rolle neuer volkssprachlicher Formen von idea für die Aufklärung gaben Descartes und Locke, für deren Philosophie bei aller Gegensätzlichkeit idee bzw. idea Schlüsselwörter sind. In Deutschland kursierten daher seit der Wende vom 17. zum 18. Jahrhundert in zahlreichen Texten die lateinischen, englischen und französischen Formen des Wortes.

Doch erfolgte zunächst keine Verdeutschung von idea oder idee. Der damaligen Gepflogenheit deutscher wissenschaftlicher Texte entsprechend wurden vielmehr idea und idee wie viele andere lateinische oder französische Fremdwörter als wissenschaftliche Termini durch einen anderen Schriftsatz von ihrem unmittelbaren deutschen Kontext abgehoben, wobei es sogar üblich war, den lateinischen Terminus in seiner flektierten Form anzuführen. Insofern war die Verwendung des französischen Wortes idee bereits ein erster Schritt zur Verdeutschung, da hiermit die lateinischen Flexionsendungen entfielen.

Leibniz forderte zwar nachdrücklich die Schaffung einer deutschen wissenschaftlichen Terminologie, blieb aber selbst bei einer lateinischen und französischen Redaktionspraxis seiner Hauptwerke, die idea und idee in hoher Frequenz verwenden.

Als Christian Wolff Leibniz’ Forderung nach einer deutschen Wissenschaftsterminologie in die Tat umsetzte, ging es ihm um die Schaffung einer „rein deutschen“ Wissenschafts­sprache, deren Elemente er aus der deutschen Allgemeinsprache übernahm. Dieses sprachtheoretisch unterbaute Konzept einer deutschen wissenschaftlichen Terminologie schloß daher eine Übernahme von idee als Fremdwort aus, so daß Wolff den Terminus idea, den er in seiner lateinischen Redaktionspraxis laufend verwendete, im Deutschen mit Begriff und Vorstellung wiedergab. Gleichzeitig erfolgte hierbei eine Präzisierung der bei den deutschen Termini, indem Begriff den universellen klassifizierenden und abstrakten Cha­rakter einer Denkeinheit bezeichnet, Vorstellung dagegen den Gedanken als Akt der Einbildungskraft. Idea im Lateinischen umfaßte beides, ebenso wie idee im Französischen und idea im Englischen.

Begriff wurde nun in der Wolffschen Philosophie noch mehr als Vorstellung zu einem Leitwort, weil Begriff aufgrund seiner Bedeutungsdifferenzierung gegenüber Vorstellung die Denkeinheit der logischen Operationen bezeichnete. Da die Lehre vom strengen logischen Denken für die Generation seiner Zeitgenossen das hervorragende Charakteristikum der Wolffschen Philosophie war, wurde der Terminus Begriff als die Einheit des logischen Denkens zu ihrem Schlüsselwort. Die vertiefte Erkenntnis der Dinge in Form deutlicher Begriffe war während einiger Zeit in Deutschland ein Kriterium für Aufklärung. Die systematische Verwendung des Wortes Begriff galt als ein Markenzeichen des Wolffia­nismus; schließlich wurde als Äquivalent für Philosoph die Bezeichnung Begriffsforscher vorgeschlagen. Vereinzelte Ansätze einer Verdeutschung von idee traten schon in der ersten Hälfte des 17. Jahrhunderts auf, begünstigt durch die ständige Präsenz einschlägiger französischer, lateinischer und englischer Texte in Deutschland. Doch begann ein Durchbruch um die Jahrhundertmitte mit der in Deutschland erfolgenden breiten Rezeption des Sensualismus in seiner vor allem von Condillac weiterentwickelten französischen Form, bei gleichzeitiger Neubelebung des Interesses an Locke und jetzt erscheinender deutscher Übersetzung seines Hauptwerkes. Die Terminologie des französischen Sensualismus mit sehr häufiger Verwen­dung von idee wurde nicht zuletzt durch Texte von Diderot und Rousseau nach Deutschland getragen. In ihren deutschen Übersetzungen ebenso wie in der Übersetzung von Locke tritt jetzt zunehmend die neue verdeutschte Form Idee auf, neben der Beibehaltung von Begriff und weiteren Wiedergaben von idee und idea durch Bezeichnungen wie Vorstellung, Meinung, Gedanke, die als Synonyme das terminologische Bedürfnis zur semantischen Differen­zierung der intellektuellen Fähigkeiten ausdrücken.

Einen neuen wichtigen Faktor der Bezeichnungsentwicklung bringt in den 70er Jahren die Genie-Epoche, wie oft der Sturm und Drang charakterisiert wird. Als Bezeichnung der kongenialen Denkform des Genies wird Idee gewählt, nicht Begriff. Auch Wolffs Anliegen war die Entwicklung der Kreativität des Denkens, doch stand für ihn die Erarbeitung von Methoden einer Objektivierung der Denkprozesse im Vordergrund, daher in seinem Werk das Gewicht der Logik und der deduktiven Methode mit ihren Definitionen und Paragraphen, jene Denkschulung, die nach Kants Worten den Deutschen ihre berühmte Gründlichkeit beigebracht hat.

Für die neue Generation, deren Energie nicht zuletzt durch Wolffs Philosophie freigesetzt wurde, mußte deren strenge Methode, die noch dazu in einer sterilen Schulbildung mit unzähligen Wiederholungen der Lehre des Meisters erstarrt war, zur Fessel weitergehender Entfaltung der Kreativität des Denkens werden. Begriff war durch lange Verwendung abgenutzt und mit der Konnotation eines Logizismus versehen, der nicht mehr an der Mode war. Das neue Wort Idee dagegen bot sich in dieser Situation an, um das intuitive Denken des Genies zu bezeichnen. In diesem Sinne ordnet auch Kant dem Genie die Idee zu, allerdings ohne etwa auf die Verwendung von Begriff zu verzichten. Damit ist die weitere Entwicklung im Deutschen vorgezeichnet: während Verdeutschungen wie Verge­sellschaftung der Begriffe anstelle von Ideenassoziation oder Weltweisheit anstelle von Philosophie wieder ganz verdrängt wurden, hat der aus dem Französischen übernommene Terminus Idee die deutsche Wissenschaftsterminologie und die Allgemeinsprache bereichert, ohne die Beibehaltung und weitere wichtige Rolle der Termini Begriff und Vorstellung in Frage zu stellen, die Christian Wolff als Wiedergabe von lat. idea vorgeschlagen hatte.

 

Vortrag am 9.11.1990, Öffentliche Gesamtsitzung
Hans Wußing (Leipzig), Ordentliches Mitglied der Mathematisch-naturwissenschaftlichen Klasse:

„Adam Ries – Rechenmeister und Cossist“

Adam Ries (1492–1559) besitzt im deutschsprachigen Raum einen geradezu sprichwört­lichen Ruf als Rechenmeister und Verfasser geschickt aufgebauter und daher immer wieder nachgedruckter Rechenbücher, die ihm den Ehrennamen „Rechenmeister des deutschen Volkes“ erwarben. Es ist jedoch kaum bekannt, daß Ries auch einer der herausragenden Repräsentanten der Deutschen Coß war, also einer Übergangsperiode in der Entwicklung der Mathematik zuzuordnen ist, die schließlich im 17. Jahrhundert in die Etablierung der Algebra als einer zweiten selbständigen mathematischen Disziplin – neben der Geometrie – mündete.

In diesem Sinne stellte sich der Vortrag das Ziel, die Rolle des Algebraikers Ries im Vergleich zu der des Rechenmeisters Ries herauszuheben und somit ihm volle historische Gerechtigkeit zuteil werden zu lassen.

Nach einigen Ausführungen zu den relativ wenigen quellenmäßig belegbaren Stationen des Lebens und Wirkens von Ries, vor allem in Erfurt und in Annaberg im sächsischen Erzgebirge, und einer Bestandsaufnahme samt Kurzcharakterisierung seiner drei wesentlich verschiedenen Rechenbücher, die das Rechnen „auf den Linien“ (Abacus, Rechentisch) und das Rechnen „auf der Feder“ (schriftlich, mit den indisch-arabischen Ziffern) behandeln, wurden im Vortrag die zwei cossischen Handschriften von Ries ausführlich vorgestellt und analysiert, die unter dem Titel „Coß“ im 17. Jahrhundert zusammengefügt worden sind. Diese eigenhändig von Ries verfaßte Schrift umfaßt 534 Seiten, ist nie gedruckt worden, war lange verschollen, ist erst im 19. Jahrhundert durch erzgebirgische Heimat­forscher wiedergefunden worden und befindet sich nun an historischer Stätte im Erz­gebirgsmuseum Annaberg-Buchholz.

Der Vortrag betonte an Hand von durchgerechneten Originalaufgaben von Ries den prinzipiellen Unterschied zwischen dem Rechenmeister Ries und dem Algebraiker Ries hinsichtlich der jeweils verwendeten mathematischen Methoden. In den Rechenbüchern verwendete Ries, darin anderen Rechenmeistern seiner Zeit ganz ähnlich, neben den elementaren Grundrechenarten und dem Dreisatz – im wohl­verstandenen Interesse seiner Leser und der Bedürfnisse der Praxis – ausschließlich die sog. Regel des falschen Ansatzes („regula falsi“) zur Behandlung von Aufgaben, die wir heute als auf lineare Gleichungen und Gleichungssysteme führend einordnen würden. Die regula falsi stellt uraltes mathematisches Erbgut dar und beruht auf einer Art systematischen Probierens zum Auffinden der Lösungen von Gleichungen. Unter Beachtung einer leicht erlernbaren und schematisch handhabbaren Rechenanweisung besitzt sie, bei linearen Gleichungen zumal, sogar eine erhebliche Reichweite.

In der „Coß“ dagegen erweist sich Ries, wissenschaftlich voll auf der Höhe stehend, als echter Algebraiker. Hatte der muslimische Gelehrte al-Chwarizmi (9. Jh.), allerdings noch verbal, eine Klassifizierung der algebraischen Gleichungen ersten und zweiten Grades vorgenommen und Lösungsmethoden angegeben, so hatten seine algebraischen Denkweisen seit dem 13. Jahrhundert allmählich auch in Europa Fuß gefaßt. In diesen Traditionen stehend und sich ihrer wohl bewußt verwendet Ries, wie zeitgenössische Cossisten, feststehende Bezeichnungen für die Potenzen der Variablen, bildet Gleichungen, klassifiziert sie und gibt abstrakte Regeln zur Auflösung von acht Typen linearer, quadratischer, rein kubischer und anderer Gleichungen und unterwirft schließlich eine Fülle von mehr als 500 Aufgaben algebraisch-cossischer Behandlungsweisen.

Ries hat seine beiden Manuskripte zur Coß nicht zum Druck bringen können. Seine Zeitgenossen schon und spätere Generationen vermochten ihn daher nur zu würdigen als Verfasser vorzüglicher Rechenbücher und Autor hervorragender – Stifel sagt: „holdseliger“ – Aufgaben; die Leistung des Cossisten Ries mußte dagegen weitgehend unbekannt bleiben. Aus Anlaß des 500. Geburtstages von Adam Ries im Jahre 1992 wird durch das Entgegenkommen der Teubner Verlagsgesellschaft Leipzig/Stuttgart und mit Unterstützung durch die Stadt Staffelstein, in der Ries geboren wurde, die „Coß“ von Ries erstmals im Druck erscheinen, versehen mit ausführlichen Kommentaren von W. Kauzner (Regensburg) und H. Wußing (Leipzig).

 

Vortrag am 12.10.1990
Nikolaus Joachim Lehmann (Dresden), Ordentliches Mitglied der Mathematisch-naturwissenschaftlichen Klasse:

„Leibnitz’ Rechenmaschine in Hannover“

Im Leibniz-Archiv der Niedersächsischen Landesbibliothek in Hannover wird die welterste mechanische Rechenmaschine für die getriebemäßige Ausführung aller vier arithmetischen Grundoperationen als eine Kostbarkeit besonderen Ranges bewahrt. Sie ist eine Erfindung des Universalgelehrten Gottfried Wilhelm Leibniz (1646–1716) und wurde noch unter seiner Anleitung gebaut. Nach seinem Tode verschollen, wurde das Gerät im vorigen Jahrhundert in Göttingen wiedergefunden und 1894–1896 vom Rechenmaschinenfabrikanten Arthur Burkhardt restauriert. Über die Funktionsfähigkeit der Maschine finden sich dabei in der Literatur sehr gegensätzliche Aussagen, die meist ohne ausreichende Begründung getroffen werden.

Im Vortrag wurden Ergebnisse vorgestellt, die sich gelegentlich eines Nachbaues der Leibniz-Rechenmaschine¹ in Dresden ergaben und die neue Einsichten in das Wirken von Leibniz als Ingenieur vermitteln. Vorangestellt werden Erfahrungen beim Studium seiner Erfindung des Sprossenrades, eines wichtigen Details für Rechenmaschinen, die aber bereits seinen Arbeitsstil gut erkennen lassen.

Das ist ein Zahnrad, bei dem zur Repräsentation der Ziffern 0 bis 9 wahlweise ebenso viele Zähne herausgestellt und somit in einem Getriebewerk verarbeitet werden können. Im Nachlaß von Leibniz findet sich hierzu ein einziges Blatt, das einen solchen Mechanismus darstellt und seinen Zweck mit den Worten „Dens mobiles d’une Roue de Multiplication“ eindeutig kennzeichnet. Trotzdem muß der Ingenieur und Kommentator Wilberg der Leibniz’schen Schriften zu Rechenmaschinen etwas resignierend feststellen: „ … Neun Segmente, die miteinander durch eine radiale Stift-Lochverbindung zu einer Kette verbunden scheinen, … . An jedem Segment ist ein radialer Zahn angedeutet. Die neun Zähne der Segmente sollten offenbar durch eine nicht ersichtliche Einstellvorrichtung wahlweise radial herausgestellt werden. Wie das geschehen sollte, wurde L. vielleicht selbst nicht klar … “. Tatsächlich kann der Mechanismus sofort verstanden werden, wenn der zur Skizze gehörige mathematisch-logische Grundgedanke erfaßt wird: mit einem herausgestellten Zahn wird zufolge der Stift-Loch-Verbindung und -Verkettung auch der (im Gegenuhrzeigersinn) vorhergehende und werden damit alle vorhergehenden Zähne herausgeschoben und fixiert. Aus dieser Grundidee sind sogleich alle in der Skizze noch offengebliebenen Fragen zwangsläufig abzuleiten, für Leibniz bedürfen sie damit keiner Erwähnung. An Hand eines nach dieser Idee gebauten Musters des Sprossenrades läßt sich des­sen sichere Funktionsfähigkeit nachprüfen. Gleichzeitig zeigt der Vergleich mit der Leib­niz’schen Ideenskizze, daß bis zur Fertigung des Gerätes noch sehr viel konstruktive Ingenieurarbeit zu leisten war. Dabei muß die vollständige gedankliche Erfassung der Leibniz’schen Lösung vorausgesetzt werden.

2. Die Leibniz’sche Rechenmaschine
Bei der Untersuchung der Nachbauten der Leibniz-Rechenmaschine in Braunschweig und München wurde deutlich, daß diese Maschinen nicht einmal die Additionsoperation wirklich vollautomatisch und immer richtig ausführen konnten. Später bestätigte sich das gleiche für das Originalgerät in Hannover. Das geht zudem aus dem Protokoll zu den Restaurations­arbeiten hervor, die von Burkhardt im vorigen Jahrhundert geleistet wurden. Die Ursachen für diesen Fehler liegen bereits im Additionsmechanismus. Zur Beschleu­nigung der Multiplikation und Division soll jede Addition (2-er Dezimalzahlen in üblicher Positionsschreibweise) bereits mit einer einzelnen Umdrehung (U = 360°) des Antriebes ausgeführt sein. Leibniz sieht erstmalig einen Ablauf in 2 Phasen vor: im 1. Schritt werden gleichzeitig (parallel) nur die zueinander gehörenden Ziffern der Summanden addiert und dabei eventuelle Übertragsziffern (in die nächsthöhere Position) in Speicherelementen abgelegt. Im 2. Schritt werden die Überträge bei der kleinsten Position beginnend nachein­ander (seriell) zu den jeweils davor liegenden Ziffern des Zwischenresultates hinzuaddiert und es wird damit die Endsumme erhalten. Im Leibniz-Rechner benötigt der 1. Schritt maximal 9 x 22,5° = 202,5° der Antriebsumdrehung. Jeder Zifferneinheit stehen also 22,5° zu; für den 2. Schritt bleiben 360° - 202,5° = 157,5°.

Burkhardt entwickelte bei der Restaurierung (teilweise Rekonstruktion) der Leibniz-­Maschine 1894 eine „Theorie“, derzufolge die Abarbeitung eines Übertrages im 2. Schritt 22,5° der Antriebsdrehung erfordert – ebensoviel wie im 1. Schritt die Verarbeitung einer Zifferneinheit. Beim 8-stellig ausgelegten Addiator der Maschine sind das zusammen mit dem 1. Schritt (202,5 + 8 x 22,5)° = 382,5°, also mehr als mit einer vollen Drehung des Antriebes zur Verfügung steht. Die Maschine konnte demzufolge niemals voll funktionsfähig sein.

Burkhardt war bei seinen Überlegungen offensichtlich von Erfahrungen mit der in seiner Fabrik hergestellten eigenen Maschine ausgegangen. Die sorgfältige Auswertung der Leibniz’schen Manuskripte und Briefe und das Gerät selbst ergeben ein anderes Bild: die beiden Schritte, Ziffernaddition ohne Übertragsverarbeitung und nachfolgende Übertragsbe­handlung sind weitgehend unabhängig. Wie beim Sprossenrad sind in Leibniz’ Skizzen und Erläuterungen zur Rechenmaschine die Arbeitsprinzipien der Maschine ohne genaue Angaben über Hebelverhältnisse und Konstruktionsdetails festgelegt. Nach den am Gerät realisierten Abmessungen ist jedoch der Winkelbedarf am Antrieb zur Ausführung eines Übertrags deutlich kleiner als 22,5°! Mit der eingebauten zusätzlichen Ausnutzung von Federkräften (mit Federn zum Einrasten), deren Wirkung in Leibniz’ Schriften besonders betont wird, genügen schon weniger als 12° und am Originalgerät wurden 10° ermittelt. Damit mußte die einwandfreie Funktion des Mechanismus auch unter Berücksichtigung unvermeidlichen mechanischen Spiels und anderer Bedingungen möglich sein. Dabei sind nur die Staffelungen der Antriebshebel für die Übertragsausführungen (die entsprechend ihrer jeweiligen Position zeitlich nacheinander erfolgen müssen) passend zu „justieren“. Tatsächlich waren lediglich die für den Antrieb der Übertragselemente vorgesehenen Doppelhebel (bei Leibniz die „Zweihörner“) passend zu spreizen, danach führte der Dresdner Nachbau der Leibniz-Rechenmaschine alle vier Grundpositionen auch mit vorzeichen­behafteten Zahlen völlig einwandfrei aus.

3. Schlußfolgerungen
Die Erfahrungen am Dresdner Nachbau der Leibniz-Rechenmaschine bestätigen die Tragfähigkeit der Leibniz’schen Erfindungen zur Rechenmaschine auch in allen Details. Der Vergleich mit der Originalmaschine bestätigt, daß die Handwerkskunst um das Jahr 1700 den dabei geforderten Fertigungsgenauigkeiten durchaus entsprechen konnte.

Wie auch für das Sprossenrad sind aber seine Ideenskizzen und Erläuterungen zur Maschine niemals Konstruktionsanweisungen, sondern sie verlangen ein Mitdenken und das Ableiten der damit implizit festgelegten Bedingungen. Die ingenieurmäßige Aufbereitung obliegt, trotz gelegentlicher mündlicher oder schriftlicher Hilfestellungen, den am Gerät beschäftigten „Werkmännern“. Ob der letzte Bearbeiter zu Leibniz’ Zeiten oder ob der Restaurator die falsche Staffelung der Übertrags-Antriebshebel zu verantworten hat, kann z.Z. nicht völlig geklärt werden. Auf jeden Fall wurden die in Leibniz’ Prinzipien implizit enthaltenen Lösungswege nicht erkannt. Außerdem ist die Maschine zu Leibniz’ Lebzeiten nicht endgültig fertig geworden. Ansonsten wäre bei Testarbeiten sicher aufgefallen, daß durch zu lange Schaltzähne für die Speicherung von Überträgen im 1. Schritt der Addition gelegentlich Fehler ausgelöst werden. Die Maschine in Hannover hat so niemals fehlerfrei gerechnet. Trotzdem, Gottfried Wilhelm Leibniz erweist sich auch im technischen Bereich als tiefer Denker mit seiner Zeit weit vorauseilenden Ideen. Aber ihm fehlte für ihre praktische Ausführung ein kongenialer Ingenieur-Mechaniker, der die von ihm völlig unterschätzten Konstruktionsarbeiten ausgeführt hätte – hier war sein Können begrenzt. Das schmälert keine seiner Leistungen, und die Leibniz-Rechenmaschine ist vielleicht gerade darum ein bewundernswertes Ergebnis.

¹ Mit freundlicher Unterstützung durch ihre Leiter wurden hierzu Modellaufnahmen von Nachbauten der Leibniz-Rechenmaschine im Landesmuseum in Braunschweig und dem Deutschen Museum in München angefertigt.

 

Vortrag am 12.10.1990
Gerhard Dudek (Leipzig), Ordentliches Mitglied der Philologisch-historischen Klasse:

„Metamorphosen von Mephistopheles und Faust bei Puschkin“

Die Beziehungen Puschkins zu Goethe sowie zu dessen „Faust“ sind seit H. Koenigs „Litterarischen Bildern aus Rußland“ (1837) und K. A. Varnhagen von Enses Puschkin­-Aufsatz (1938) Gegenstand zahlreicher Untersuchungen von Literaturkritikern, Slawisten und Germanisten. Dennoch weist dieses Forschungsfeld immer noch Lücken auf. Dazu gehört eine das Gesamtschaffen Puschkins berücksichtigende Darstellung der Rezeption und schöpferischen Umsetzung der Faustsage durch den Autor des „Eugen Onegin“.

In unserer Studie gehen wir davon aus, daß Puschkin Kenntnis vom Volksbuch über Faust, von Fr. M. Klingers Roman „Fausts Leben, Taten und Höllenfahrt“ sowie Goethes „Faust“ (Erster Teil) erhalten hat, sei es aus mündlichen Berichten bzw. französischen Übersetzungen und deutschen Originalen. Unter dem Eindruck des Faust-Kapitels in Mme. de Staëls „De l’Allemagne“ gewann Goethes Mephistopheles für Puschkin besondere Bedeutung, da diese Gestalt seiner geistigen Haltung um 1820 entgegenkam und ihn auch später immer wieder zur Darstellung reizte. Dies belegen wir zunächst damit, daß Puschkin wahrscheinlich bereits 1821 Mephisto­pheles – allerdings noch in der Figur des Teufels der christlichen Dämonologie – reflektiert hat. Dafür spricht, daß der Dichter auf dem Blatt mit dem Plan für das Poem „Gabrieliade“ ein Porträt zeichnete, das von M. A. Zjawlowski als das Goethes angesehen wird. Das zeigt sich ferner an den Fragmenten des Poems „Der verliebte Teufel“ (1821) sowie den zu diesem Sujet entworfenen „Höllenzeichnungen“, zu denen Puschkin offenbar durch Szenen aus Klingers Faust-Roman angeregt worden ist.

Die Metamorphose des religiösen Teufels zu einer weltlichen Gestalt philosophisch­politischen Inhalts postulieren wir – Beobachtungen D. Gerhardts folgend – für einen Zyklus von sieben Gedichten und Versfragmenten, die vornehmlich Ende 1823 in Odessa entstanden sind. Mit der Figur des Dämon in dem gleichnamigen Gedicht vom Oktober/November 1823 schuf Puschkin eine eigenständige Variante zu Goethes Mephistopheles, die für die russische Literatur ebenso bedeutsam werden sollte wie Goethes Schöpfung für die deutsche. In Puschkins eigener Deutung seines „Dämon“ als „Geist der Verneinung“ sehen wir allerdings aus chronologischen Gründen einen nachträglich hergestellten Bezug zu Goethes Mephisto.

Den Schwerpunkt unserer Untersuchung bilden Puschkins „Szene aus dem Faust“ sowie die fragmentarischen „Skizzen zu einem ,Faust‘“, die 1825/26 in Michailowskoje verfaßt worden sind. Das Versfragment „Sag mir, durch welche Zaubersprüche“ wird von uns als selbständiger Entwurf und als Vorstufe zur „Szene aus dem Faust“ betrachtet. Mit der Analyse dieser „Szene“ erhellen wir die Wandlungen von Mephistopheles, der tragenden Gestalt des Werkes, vom Philosophen der Langeweile über den Psychologen und Moralisten zum Tatmenschen, der Fausts Befehl vollstreckt. In Puschkins Faust sehen wir dagegen mehr eine Folie für Mephistos Metamorphosen, von der sich die Phänomene der existentiellen Langeweile und eines für die russische Literatur charakteristischen ethischen Maximalismus deutlicher abheben. Das Schlußbild der „Szene“ wird von uns als Ansatz zu einem historischen Verständnis der Faustgestalt durch Puschkin gedeutet. Puschkins „Szene aus dem Faust“ als Ganzes genommen wird insofern als eigenständige Variante des Faust-Stoffes gewertet, als Faust darin anders als sonst motiviert erscheint – nicht durch Wissensdurst und Lebenshunger, sondern durch ständiges Unbefriedigtsein mit allen Verlockungen und Genüssen des Lebens, das in der menschlichen ratio seine tiefste Wurzel besitzt.

In einem Exkurs erörtern wir die Frage, ob Goethe von Puschkins „Szene aus dem Faust“ gewußt hat und ob ein Zusammenhang zwischen dem Schluß dieser „Szene“ und dem V. Akt von Goethes „Faust II“ besteht. Die „Skizzen zu einem ,Faust‘“ werden von uns als extravertierter, im Ansatz gesellschafts­bezogener Gegenentwurf zur introvertierten „Szene aus dem Faust“ interpretiert. Ihre möglichen Bezüge zu Goethes „Walpurgisnacht“, Dantes „Hölle“ und zum Volksbuch über Faust werden kritisch beleuchtet. Nach 1826, so zeigen wir, reflektierte Puschkin Goethes Tragödie in seinen literaturkriti­schen Äußerungen vor allem als literaturhistorische, maßstabsetzende Erscheinung. Faust und Mephistopheles erhielten in seinem dichterischen Schaffen nur noch Zeichenfunktion, sei es unter psychologischem („Pique Dame“) oder sozialhistorischem Aspekt („Szenen aus der Ritterzeit“).

Puschkins Darstellungen von Mephistopheles und Faust werden als eigenständiger Beitrag zur philosophisch-existentiellen bzw. volkstümlich-gesellschaftskritischen Linie in der europäischen Faust-Literatur gewertet. Mit ihnen eröffnete er die Reihe der russischen Fausts bei W. Odojewski, Turgenjew, Dostojewski, Gorki, Lunatscharski, Lewada u.a. sowie andererseits die Hypostasierungen des „phiolosophischen Teufels“ – sei es als Dämon oder Mephistopheles – bei Lermontow, Dostojewski, F. Sologub, Bulgakow u.a.

Vortrag am 8.6.1990
Klaus Arnold (Leipzig), Ordentliches Mitglied der Mathematisch-naturwissenschaftlichen Klasse:

„Oberflächenkräfte und ihre Bedeutung für biologische Prozesse“

Das Studium biologischer Prozesse hat immer wieder Fragen sehr grundsätzlicher Natur an die Physik gestellt. Zu einem solchen Problem führten die Untersuchungen der Fusion von Zellen, intrazellulärer Fusionsprozesse (Exo- und Endozytose) und der Virus-Zell-Fusion. Es hatte sich herausgestellt, daß eine solche Fusion nur auftreten kann, wenn eine Annäherung der Membranen bis zum molekularen Kontakt der Oberflächen auftritt. Normalerweise sind Zellen gegen eine solche Annäherung durch die Existenz von ab­stoßenden Kräften zwischen ihren Oberflächen geschützt. Solche Kräfte waren in den Kolloidwissenschaften für die Wechselwirkung kleiner Teilchen zwar schon beschrieben worden, aber es fehlten Daten über diese Kräfte bei kleinen Abständen der Oberflächen. Es gab Hinweise, daß eine unerwartet hohe Abstoßung auftritt. Dadurch wurde die Frage nach dem Ursprung dieser Kräfte völlig neu aufgeworfen, und schließlich mußten auch Methoden entwickelt werden, die eine direkte Messung dieser Kräfte in Lösungen erlauben. Auf diesem Gebiet sind in den letzten 10 Jahren bemerkenswerte Fortschritte erzielt worden.

Die Untersuchungen an Membransystemen zeigten, daß für Abstände unter 2 nm neben der elektrostatischen Abstoßungskraft und der van der Waals-Anziehung eine weitere Abstoßungskraft auftritt, die als Hydratationskraft bezeichnet wird. Wir haben die NMR-­Methode zur direkten Messung dieser Kraft als Funktion der Dicke der Wasserschicht zwischen den Membranen benutzt. Die Hydratationskraft resultiert aus der Orientierung von Wassermolekülen an der Membranoberfläche und übertrifft die elektrostatische Abstoßung um mehrere Größenordnungen bei kurzen Membranabständen. Daraus ergibt sich, daß die Hydratationskräfte die wichtigste Barriere für die Annäherung der Membranen und deren Fusion darstellen.

Untersuchungen von natürlichen Fusionsprozessen erbrachten Hinweise dafür, daß die Hydratationskräfte durch die Hydrophobisierung der Oberfläche reduziert werden. Eine wichtige Rolle bei der Auslösung von Fusionsprozessen spielen Erhöhungen der Ca²⁺­-Konzentration. Unsere Untersuchungen zeigen, daß die Bindung der Ionen an die Membran durch eine starke Erniedrigung der hydrophilen Eigenschaften der Oberfläche begleitet wird. Ähnlich wirken wahrscheinlich spezifische, fusionsfördernde Proteine. Ihre Funktion ist bisher am besten für die Fusion von Viren (z.B. Influenza, Sendai, HIV) mit Zellen untersucht worden. Die dazu durchgeführten Untersuchungen zeigen, daß die Fusion der Virushülle mit der Zellmembran durch eine Konformationsänderung von Proteinen in der Virusoberfläche eingeleitet wird, wodurch hydrophobe Oberflächenbereiche gebildet werden und die Hydratationsabstoßung zu einer Anziehung umgeschaltet wird.

Daraus ergeben sich Möglichkeiten für die Entwicklung von Pharmaka, deren Wirkung auf die Virusinfektion in der Hemmung der Fusionsprozesse besteht. Eine bemerkenswerte Eigenschaft der Hydratationskräfte besteht darin, daß sehr kleine Änderungen der Ober­flächeneigenschaften, die beispielsweise durch Ionenbindung oder geringe Konformations­änderungen der Proteine ausgelöst werden, ihre Größe total verändern können. Außer bei den Fusionsvorgängen kann die Natur diesen „Trick“ sehr wirksam zur Regulation von Prozessen einsetzen. Diese Kräfte sind deshalb nicht nur als eine neue, universelle Oberflächenkraft anzusehen, sondern sie sind auch hinsichtlich ihrer Bedeutung für eine Vielzahl biologischer Prozesse weiter zu untersuchen. Aus der Sicht der Physik ist die Ausarbeitung einer Theorie der Hydratationskräfte entscheidend von den Fortschritten der theoretischen Beschreibung der flüssigen Phase abhängig. Die Erklärung der Hydratationskraft muß in den Strukturveränderungen in der Flüssigkeit gesucht werden, die durch die Teilchenoberfläche induziert werden und nicht durch Kontinuumsbehandlungen beschreibbar sind.

 

Vortrag am 8.6.1990
Gotthard Lerchner (Leipzig), Ordentliches Mitglied der Philologisch-historischen Klasse:

„Kommunikationskultur im europäischen Kontext. Zur Entwicklung der deutschen Sprache im 18. Jahrhundert“

Der Bericht über ein Forschungsprojekt zur Sprachgeschichte des Deutschen im 18. Jh. (Laufzeit: 1990–1995) stellte in einem ersten Teil ein neuentwickeltes sprachhistoriogra­phisches Modell vor, das in bezug auf die entwicklungsgeschichtliche Spezifik des Untersu­chungsgegenstandes greifen soll. Es nimmt Grundgedanken des kulturmorphologischen Forschungsansatzes von Th. Frings und der Kultursemiotik der Tartuer Schule (J. M. Lotman) auf, insofern diese eine prinzipielle Interaktion von Sprachsystem(en) und anderen Sozialsystemen, deren wechselseitige Bedingtheit, die tendenzielle Gleichgerichtetheit ihrer historischen Bewegungsabläufe und ihre gegenseitige Beeinflußbarkeit im Rahmen von systematisch organisierten unterschiedlichen Domänen des Sozialverhaltens unterstellen. Diese ,Domänen des Sozialverhaltens‘ können im konstruktivistischen Theorierahmen der Systemtheorie (u.a. Luhmann, Hejl, S. J. Schmidt) als Netzwerk von Sozialsystemen, d.h. als die Gesamtheit von kognitiven und sozial-strukturellen (Teil-)Systemen gefaßt werden, auf die menschliches Handeln angewiesen ist.

Beschreibungspraktisch umsetzbar wird dieses Konzept mit Hilfe der Kategorie Kommu­nikationskultur (nach Hymes u.a.), insofern nach deren Vorgaben die Regeln einer Kultur in bestimmten Grenzen festlegen, wer mit wem bei welchen Gelegenheiten in welchen Formen über welche Inhalte „regelhaft“-durchschnittlich kommuniziert. Die sprachhistorio­graphische Applikation der Kategorie im Rahmen des systemtheoretisch orientierten Analyseansatzes wird auf drei Konsequenzen hin bedacht:

1. Linguistischer Ort jeglichen Sprachwandels ist demnach das sprachhandelnde Individuum im Knoten heterarchisch organisierter Sozialsysteme. Es ist demgemäß zu verfolgen, ob und inwieweit eine direkte proportionale Beziehung besteht zwischen dem Grad der funktionalen Differenzierung des Konsoziums einerseits und dem Grad der Individualisierung sprachlichen Verhaltens andererseits. Bei Bestätigung einer entsprechenden Hypothese wäre das 18. Jh. in der (mittel)deutschen Kommunikationsgeschichte zu charakterisieren durch den epochen­spezifischen Aufstieg des (bürgerlichen) Individuums in der Sprachkommunikation. Das zieht die Forderung nach sich, den historischen Diskurs (verstanden als Textexemplar in der sozialen Interaktion) in seiner unikalen Spezifik zu untersuchen; dazu bedarf es der Analyse eines umfangreichen, sorgfältig auszuwählenden empirischen Materials aus zeit­genössisch signifikanten Bereichen des Textsortenspektrums.
2. Die Beschreibung der epocheneigentümlichen Kommunikationskultur hat die Parameter zu spezifizieren, die sich mit dem Sozialsystem Sprache in Wechselbeziehung befinden.
3. Um die soziokulturellen Interpenetrationen hinsichtlich ihrer sprachgeschichtlichen Auswirkungen manifest ma­chen zu können, wird ein disziplinspezifisches Instrument benötigt, das auf Grund seiner funktionellen Beschaffenheit die Möglichkeit bietet, den Austausch zwischen verschiedenen Sozialsystemen einerseits mit dem System ,Sprache‘ andererseits verfolgbar zu machen. Als dieses Instrument wird die Textkategorie in Anspruch genommen, und zwar in dem von Coseriu und Schlieben-Lange introduzierten Verständnis. Danach ist ein Text und ist demzufolge auch Textgeschichte ein kulturelles bzw. kulturgeschichtliches Phänomen, inhaltlich und strukturell determiniert durch Parameter einer sprachübergreifenden kultu­rellen Gemeinschaft. Das betrifft Textmuster (als types).Daher hat der Untersuchungsansatz die Testsortenzugehörigkeit im untersuchten Raum zur gemeinsamen Kulturentwicklung in Westeuropa substantiell als entscheidenden Aspekt der Aufgabenbemessung zu berück­sichtigen: Kommunikationskultur im Deutschland des 18. Jh.s kann nur erforscht werden im europäischen Kontext, beschreibbar über Textmusterin(ter)ferenzen.

Der gleiche Sachverhalt betrifft aber auch Textmusterrealisierungen (tokens). Die Einbindung des kommunizierenden Individuums in heterogene Sozialsysteme hat in der Kommunikation Textmustermischungen zur Folge. Im Untersuchungsprogramm stellt die analytische Sicherstellung der konkreten Erscheinungsformen dieser Mustermischungen in unterschiedlichen Textbereichen daher eine wichtige Aufgabe dar.

In einem zweiten Teil des Vortrages wird die Praktikabilität des theoretisch-me­thodologischen Konzepts an hand von Untersuchungsergebnissen zu Ch. M. Wielands sprach- bzw. literaturkritischen Äußerungen im „Teutschen Merkur“ darzustellen versucht.

 

Vortrag am 4.5.1990
Armin Uhlmann (Leipzig), Ordentliches Mitglied der Mathematisch-naturwissenschaftlichen Klasse:

„Ja oder nein – wie es in der Quantenphysik funktioniert“

Die elementare Alternative, die durch Fragen wie ‚ja oder nein‘, ‚Eins oder Null‘, ‚richtig oder falsch‘, … usw. ausgedrückt wird, ist nicht nur eine der einfachsten logischen Strukturen. Sie ist auch in physikalischen Systemen realisiert, z.B. in Schaltern, die (cum grano salis) nur zweier Zustände fähig sind, ‚Ein‘ und ‚Aus‘.

Freilich ist ein System, bei dem nur zwei Zustände unterschieden werden, trivial, da es ihm an Struktur mangelt. Interessante Systeme können viele verschiedene Zustände einnehmen. Dann erweist es sich als notwendig, zwischen Zuständen und beobachtbaren Größen (Observablen) zu unterscheiden, wobei diese beiden Begriffe erst durch ihr Zusammenwirken mit nachprüfbarem Inhalt ausgestattet werden: Ein physikalisches System ist verschiedener momentaner Zustände fähig, deren Gesamtheit seinen Zustandsraum ausmacht. Die Observablen weisen Zuständen Meßwerte zu und hierdurch können Zustände unterschieden werden. Umgekehrt dürfen nur dann zwei Zustände als verschieden gelten, wenn es mindestens eine Observable gibt, die sie als verschieden zu erkennen erlaubt.

Nichts erscheint einleuchtender als die Behauptung, daß mit zwei Ja-Nein-Fragen (mit zwei Schaltern) vier Zustände unterschieden werden können, nämlich (ja, ja), (nein, nein), (ja, nein) und (nein, ja). Dies ist jedoch nicht notwendigerweise so: Zwei Ja-Nein-Fragen können unverträglich, d.h. simultan nicht abfragbar sein. Bohr hat eine solche Situation mit dem Begriff der Komplementarität zu beschreiben versucht und besonders an dem Observablenpaar Ort und Geschwindigkeit (bzw. Impuls) erläutert. Heisenberg hat diese eigenartigen Situationen auf die Nichtvertauschbarkeit derjenigen Größen zurückgeführt, die in den Rechnungen der Physik für die Observablen stehen. Er konnte so eine Art Phänomenologie in eine in sich geschlossene Theorie wandeln. Da grundsätzlich jede Observable als eine in sich verträgliche Schar von elementaren Alternativen aufgefaßt werden kann, sollte sich die Art und Weise, wie sich in einem konkreten physikalischen System die Observablen verhalten und welche Zustände sie beschreiben, vollständig auf Beziehungen zwischen Ja-Nein-Fragen abbilden lassen. Dies ist richtig, und Jordan fand, daß dieser Gedanke auf eine abstrakte Logik, eine Quantenlogik führt.

Es ist Ziel des Vortrages, das kleinste System dieser Art und einige seiner physikalischen Realisierungen vorzuführen. Nur für die Zwecke dieses Vortrages nenne ich es einen Quantenschalter. Dieses Gebilde kann man genau und ohne nennenswerten Aufwand beschreiben, wenn man auf die Darstellung der Beweisschritte verzichtet. Ein Quanten­schalter ist, kurz gesagt, ein quantenphysikalisches System, bei dem jede Observable eine Ja-Nein-Frage ist. Beliebige zwei verschiedene Observable dieses Systems sind daher unverträglich. Sie können nie simultan abgefragt werden. Man könnte sagen, sie seien sämtlich im Sinne von Bohr untereinander komplementär.

Die Zustände eines Quantenschalters korrespondieren eindeutig zu den Punkten einer Kugeloberfläche. Von seinem Zustandsraum kann man sich daher mit Hilfe eines Globus leicht ein Bild machen. Natürlich sind die Punkte dieser Kugeloberfläche nicht die Zustände selbst – so wie die Städte auf dem Globus nicht die Städte selbst sind, sondern nur ihre gegenseitige Lage korrekt wiedergeben. In diesem Sinne können für die Quantenschalter aus der Lage zweier Zustandspunkte auf dem ‚Zustandsglobus‘ die gegenseitigen Bezie­hungen der zugehörenden Zustände abgelesen werden. Z.B. sind Zustände, die auf dem Zustandsglobus näher beieinander liegen, ähnlicher als weiter voneinander entfernte.

Nach der Menge und Lage der Zustände komme ich jetzt zu den Observablen des Quantenschalters. Hierzu nenne ich jede Gerade, die durch den Mittelpunkt der Kugel geht und daher die Kugeloberfläche in genau zwei Punkten schneidet, eine ‚Achse‘. Jede Achse symbolisiert eine elementere Alternative, eine Ja-Nein-Frage. Sie fragt nämlich, ob einer der beiden Zustände vorliegt, die durch die beiden Schnittpunkte der Achse mit der Kugelober­fläche gegeben sind. Jede Ja-Nein-Frage testet somit zwei Antipoden der Kugeloberfläche, des Zustandsglobus. (Genau genommen sind es jeweils zwei voneinander völlig abhängende Fragen je nachdem bei welchem der beiden Antipoden die Antwort ‚Ja‘ lauten soll. Man muß der Achse also noch eine Richtung vom ‚Nein‘ zum ‚Ja‘ zubilligen.)

Das von den klassischen Vorstellungen so vollständig Verschiedene verbirgt sich in der Feststellung, daß es keine anderen beobachtbaren Größen für einen Quantenschalter gibt als die eben definierten, welche durch die Symmetrieachsen (bzw. Antipodenpaare) der Kugeloberfläche bestimmt sind. Um dies logisch unanfechtbar zu machen, muß man nach Born grundsätzliche Unbestimmtheiten zulassen, die lediglich von Wahrscheinlichkeiten regiert werden. Diese Wahrscheinlichkeiten sind innerhalb des jeweiligen physikalischen Systems unveränderbar und können durch Einbettung in ein größeres System höchstens verkleinert, die in Rede stehenden Unbestimmtheiten also höchstens vergrößert werden.

Wie entstehen beim Quantenschalter die Unbestimmtheiten? Hierzu nehme ich an, auf dem Zustandsglobus würde die Frage gestellt: Nordpol (Ja) oder Südpol (Nein). Was geschieht, wenn im physikalischen System keiner dieser beiden Zustände realisiert war? Nun, die Antwort des Systems lautet mit einer gewissen a priori Wahrscheinlichkeit „Ja“:

Wiederholt man bei gleicher Ausgangslage die Messung, so wird das System manchmal und absolut zufällig mit „Ja“ und manchmal mit „Nein“ antworten. Für sehr viele Wiederholungen hängt die Rate der „Ja“-Antworten nur von der Lage des Zustands relativ zum Nordpol ab und gerade diese ‚Grenzrate‘ ist die a priori Wahrschein­lichkeit.

Diese Wahrscheinlichkeit heißt auch Übergangswahrscheinlichkeit, da sie angibt, wie groß die Erwartung ist, daß die Frage nach einem Zustand A mit ‚Ja‘ beantwortet wird, wenn sich das System im Zustand B befindet. Es handelt sich dabei tatsächlich um einen Übergang; denn als Resultat der Frage, ob der Zustand A vorliegt oder nicht, ist nach der Messung entweder der Zustand A oder sein Antipode realisiert. Jede Frage testet also nicht nur genau zwei Antipoden des Zustandsraumes, sie präpariert auch: Nach ihrer Ausführung nimmt das System mit Sicherheit einen der beiden Zustände ein, nach deren Unterscheidung gefragt wurde!

An Hand eines Globus kann man die Übergangswahrscheinlichkeit leicht angeben. Hat man zwei Zustände, A und B, so geht durch jeden genau eine Achse. Nehmen wir an, A sei der Nordpol. Drehen wir den Globus um die Nord-Süd-Achse, so beschreibt der andere Zustandspunkt, B, einen Breitenkreis. Dieser teilt die Oberfläche der Kugel in zwei Gebiete. Der Flächeninhalt desjenigen Gebietes, das den Südpol enthält, geteilt durch die Gesamt­fläche, ist genau die Übergangswahrscheinlichkeit von B nach A.

Im Vortrag werden vier physikalische Realisierungen des Quantenschalters als Beispiele genannt:

1. Das magnetische Moment (bzw. der Spin) des Elektrons, das sich in einem Magnetfeld nur in oder entgegen der Magnetfeldrichtung ausrichten kann. Die Ja-Nein-Fragen werden durch Stern-Gerlach-Versuche realisiert. Der Punkt, in dem eine Gerade in Spinrichtung die Kugeloberfläche durchstößt, ist ihr Zustandspunkt.
2. Die Polarisation des Photons. Hier können Nord- und Südpol als rechts- oder links­zirkulare Polarisation definiert werden. Der Äquator beschreibt linear polarisierte Photonen derart, daß Antipoden auf dem Äquator zu senkrecht aufeinander stehenden linearen Polarisation gehören. Die übrigen Punkte klassifizieren die elliptischen Polarisationsmoden.
3. Die Paare der Inversionslinien des Ammoniakmoleküls. Die beiden Zustände der Observablen Energie bestimmen eine Achse, die auch als Drehachse des Zustandsraumes mit der Drehgeschwindigkeit ‚Energiedifferenz geteilt durch Plancksches Wirkungsquantum‘ die Bewegung des Zustandsglobus in der Zeit beschreibt. Die Achsen der zu Ja-Nein-Fragen degenerierten Observablen ‚Ort‘ und ‚Geschwindigkeit‘ stehen senkrecht auf der Energie­achse.
4. Das Teilchen-Antiteilchen Problem des Systems der neutralen K-Mesonen. Hier werden Fragen nach dem Verhalten gegenüber der starken bzw. der schwachen Wechselwir­kung gestellt, die zwei zueinander senkrechten Achsen zugeordnet sind. Eine weitere wichtige beobachtbare Größe ist der Zerfall des neutralen K-Teilchen in zwei oder in drei π-Teilchen.
   
   
   

Vortrag am 4.5.1990
Ernst Eichler (Leipzig), Ordentliches Mitglied der Philologisch-historischen Klasse:

„Vom Schicksal der Worte: zum Werk Václav Havels“

­Für den tschechischen Schriftsteller Václav Havel (geb. 1936) ist die Vorstellung vom „Wunder des menschlichen Wortes“ der Schlüssel für das Verständnis des Menschseins in sich selbst und in der Gesellschaft. Mit Hilfe des Wortes schuf er künstlerische Werke, so seine Dramen und Essays, rief er in den Zeiten der gewaltsamen Repression zum Handeln auf, legte rituelle Kommunikation innerhalb der Machtstruktur und Anonymisierung der Macht mit all ihren Folgen bloß und leistete dagegen aktiven Widerstand unter Einsatz seines Lebens. Mit Hilfe des Wortes hoffte er auf Erneuerung, die im Jahre 1990 Wirklichkeit wurde und die er kurz davor, in seiner Rede anläßlich der Verleihung des Friedenspreises des Deutschen Buchhandels (1989), noch als Vision sah. Havels Humanismus wurzelt nicht nur in der heimischen tschechischen, im europäischen Kontext noch zu wenig bekannten Tradition (so etwa in T. G. Masaryks Sozialphilosophie und in den Vorgängern der tschechischen Literatur selbst, z.B. in den Werken K. Čapeks), sondern auch in den besten europäischen Traditionen. Die ihm eigene Verbindung von Wort und Text verleiht seinem literarischen Schaffen unverwechselbare Originalität.

 

Vortrag am 20.4.1990
Lothar Rathmann (Leipzig), Ordentliches Mitglied der Philologisch-historischen Klasse:

„Europäische Herausforderungen – arabisch-islamische Antworten. Akkulturationsprozesse im Ägypten des 19. Jahrhunderts“

Vom 8.–10. Jahrhundert, unter den Omajjaden und in der Blütezeit des Abbasidenreiches vermochte die „pax islamica“ zu generalisierenden Aspekten menschlichen Lebens vorzu­dringen und eine brücken schlagende Funktion zwischen den Kontinenten auszufüllen. Doch in den folgenden Jahrhunderten geriet die arabische Welt durch die Verkettung fortschrittsblockierender Elemente innerhalb der Region mit verheerenden Wirkungen exogener Faktoren, wie Mongolensturm, Verlagerung der Handelswege und die Herrschafts­praktiken des osmanischen Militärfeudalismus, gegenüber der Entwicklungsdynamik West- ­und Mitteleuropas in Rückstand.

Seit Beginn des 19. Jahrhunderts bestimmte in Auswirkung der Großen Französischen Revolution und der industriellen Revolution das Spannungsverhältnis zwischen dem expandierenden Europa und den auf islamischen Traditionen beruhenden sozialökonomi­schen und geistig-kulturellen Strukturen der arabischen Gesellschaft Inhalt, Tendenzen und Ergebnisse der Transformationsprozesse in Nordafrika und im Nahen Osten. Auf geistig-kultureller Ebene führte der Einbruch der Neuzeit in den Modernen Orient zu einem konfliktgeladenen Akkulturationsprozeß von Abkehr und Selbstbehauptung, in dem zwei Strömungen nach einer kreativen Antwort suchten: die frühbürgerliche arabische Aufklärung und der islamische Modernismus.

Die hervorragendsten Vertreter der arabischen Aufklärung waren der ägyptische Muslim at-Ṭahṭāwī und der libanesische Christ Buṭrus al Bustānī. Diese beiden Pioniere des muslimischen und des christlichen Flügels der arabischen Aufklärung setzten zwar ­korrespondierend mit den grundlegend differierenden Bedingungen ihrer Länder – die Akzente unterschiedlich, aber die Gemeinsamkeiten zwischen ihnen dominierten, so daß es korrekt ist, die arabische Aufklärung als eine im wesentlichen einheitliche Linie progressiven Denkens zu werten.

Im Unterschied zu den Aufklärern, die für eine partielle Adaption europäischer Errungenschaften, ohne dabei an eine Reform des Islams zu denken, war für den Inaugurator des islamischen Modernismus, Ǧamal ad-Dīn al-Afġānī, die Reform des Islams selbst Voraussetzung und Grundlage sozialer, ökonomischer und politischer Umgestaltungen. In der Bereitschaft, Elemente der westlichen Zivilisation zu übernehmen, ließ sich Afġānī sowohl von einer fundamentalistischen Interpretation des Islams als auch von einem entschiedenen, panislamisch orientierten Antikolonialismus leiten.

 

Vortrag am 2.3.1990
Klaus Beyer (Leipzig), Ordentliches Mitglied der Mathematisch-naturwissenschaftlichen Klasse:

 

„Freie Randwertprobleme in der Hydrodynamik idealer Flüssigkeiten“

Der Vortrag nimmt Bezug auf die Theorie der Gleichgewichtsfiguren rotierender, geladener, dielektrischer, magnetischer oder gravitierender Flüssigkeiten.

Die Theorie rotierender homogener Flüssigkeiten reicht zurück auf Newtons Unter­suchungen zur Erdfigur. In seinen „Mathematischen Prinzipien der Naturphilosophie“ leitet Newton durch Gewichtsvergleich zweier Flüssigkeitssäulen in Bohrungen, die vom Äquator bzw. vom Nordpol zum Erdmittelpunkt verlaufen, die Beziehung

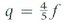
zwischen Ab­plattung f (Verhältnis der Differenz äquatorialer-polarer Radius zu äquatorialem) und dem Quotienten q von zentrifugaler und Schwerebeschleunigung am Äquator her. Daraus folgt

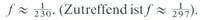
In der Folgezeit beschäftigten sich führende Mathematiker, darunter Maclaurin, Jacobi, Riemann, Poincaré, Ljapunov, Lichtenstein mit den Gleich­gewichtsfiguren. Maclaurin bewies als erster, daß bei hinreichend langsamer Rotation abgeplattete Rotationsellipsoide in dem Sinne Gleichgewichtsfigur sein können, daß die Resultierende zwischen Anziehungskraft und Zentrifugalkraft in jedem Punkt der freien Oberfläche in die Normalenrichtung weist. Äquivalent damit ist die Gleichung

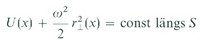
zwischen dem Newtonschen Potential U der Gleichgewichtsfigur und dem Abstand r_⊥ der Punkte x ihrer Oberfläche S von der Rotationsachse, wobei ω die Winkelgeschwindigkeit bezeichnet.

Die Theorie rotierender, durch Kapillarkräfte zusammengehaltener Flüssigkeitstropfen wurde durch die Plateauschen Experimente [J. Plateau, Recherches expérimentales et théoriques sur les figures d’équilibre d’une masse liquide sans pesanteur. Mém. Acad. Roy. Sci. Lett. Belg. 16–37 (1843–69)] mit Öltropfen in gleich dichten Flüssigkeiten angeregt. Rayleigh berechnet neben axialsymmetrischen Tropfenformen auch die Gestalt dünner rotierender Flüssigkeitsringe [Lord Rayleigh, The Equilibrium of Revolving Liquid under Capillary Force. Phil. Mag. 28 (1914), 161–170]. Appell vereinfachte die Rechnungen später und erweiterte sie durch Stabilitätsbetrachtungen. Ist β die Oberflächenspannung, dann lautet die Gleichgewichtsbedingung für den wie ein starrer Körper gleichförmig rotierenden Tropfen

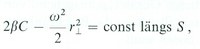
wobei C die mittlere Krümmung seiner Oberfläche S ist (positiv genommen, wenn der zugehörige Krümmungsmittelpunkt im Inneren liegt). In Verbindung mit den modernen Weltraumtechnologien sind Theorie und Experiment mit rotierenden oder oszillierenden Tropfen heute erneut ins Interesse gerückt.

Die obigen Gleichungen sind Spezialfälle allgemeinerer Gleichgewichtsbedingungen, die die Form rotierender Tropfen oder Flüssigkeitsmassen unter dem Einfluß der Oberflächen­spannung, von Eigengravitation, Ladung oder in Außenfeldern bestimmen. Die freie Oberfläche S eines inkompressiblen Tropfens T (Dichte = 1) ist durch das Prinzip der virtuellen Arbeit bestimmt, nach dem die effektive potentielle Energie E(S) ( = potentielle + Rotationsenergie) stationär bezüglich der mit den Nebenbedingungen verträglichen Variationen δS seiner Oberfläche sein muß. Wegen der Inkompressibilität der Flüssigkeit sind die Volumina |T|vorzuschreiben. Berücksichtigt man die Nebenbedingung durch einen Lagrangeschen Multiplikator, dann gelangt man zum freien Variationsproblem δ(E(S) – λ|T(S)|) = o. Z.B. ist

gilt. Die entsprechende Gleichgewichtsbedingung lautet

n bezeichnet den nach außen gerichteten Normalenvektor und γ^– bzw. γ⁺ sind die inneren bzw. äußeren Grenzwerte des magnetischen Spannungstensors.

Der Lösung der Bewegungsgleichungen stellen sich wegen ihrer hohen Nichtlinearitäten besondere Schwierigkeiten entgegen. So blieb selbst das Anfangswertproblem für den um seine Gleichgewichtslage schwingenden idealen Kapillartropfen seit Rayleigh, der 1879 die infinitesimalen Schwingungen beschrieb, ungelöst.

 

Vortrag am 2.3.1990
Reiner Groß (Dresden), Ordentliches Mitglied der Philologisch-historischen Klasse:

„Sachsen und die Wettiner – Fragen an die Geschichte eines deutschen Territorialstaates“

Das Thema wurde aus zwei aktuellen Anlässen behandelt. Einmal im Erinnern an die 900. Wiederkehr der Belehnung eines Wettiners mit der Markgrafschaft Meißen im Jahre 1989. Zum anderen in Anbetracht des wieder zu begründenden Landes Sachsen im Laufe des Jahres 1990 nach dessen faktischer Auflösung im Juli 1952.

Im Rahmen des Vortrages ist versucht worden, das Verhältnis des gegebenen historischen Raumes zunächst zwischen Saale und Elbe, später ausgreifend bis zur Werra im Westen sowie Bober und Queis im Osten zu dem Wirken und den Leistungen der in diesem Raum lebenden Menschen unterschiedlicher ethnischer Herkunft und Zugehörigkeit zu sozialen Klassen und Schichten einschließlich der Dynastie der Wettiner in herausgehobener Betrachtung tiefer auszuloten. In allen Phasen der historischen Entwicklung verkörpert sich sächsische Geschichte in der Geschichte des deutschen Volkes für über tausend Jahre, wovon der thüringisch-sächsische Raum für 829 Jahre mit den regierenden Angehörigen des Hauses Wettin, seit 1485 der ernestinischen und albertinischen Linie gleichermaßen verbunden ist.

Im weiteren Verlauf des Vortrages wurden sechs Fragen einer näheren Betrachtung unterworfen. Sie galten erstens dem Belehnungsvorgang, der erst 1882 von Otto Posse eindeutig erforscht und jüngst durch erneute Quellenforschungen zur Kanzlei Kaiser Heinrichs IV. weiter gestützt wird. Zweitens wurde der gesellschaftliche Aufstieg der Wettiner von Lebensträgern des deutschen Feudalstaates zu bedeutenden deutschen Territorialfürsten im Zusammenhang mit der Ausbildung von Landesherrschaft im Mittel­alter verbunden. Ein dritter Gedanke galt den natürlichen Ressourcen des Landes und des Umganges mit ihnen seitens der das Land bewohnenden Menschen. Viertens wurde der ethnischen Zusammensetzung der Bevölkerung sowie den Zu- und Abwanderungen mit ihren Auswirkungen auf die wirtschaftlichen und kulturellen Leistungen des Landes nachgegangen. In einem fünften Abschnitt wurde der Zusammenhang zwischen Rechts­fragen, Wirtschaftsformen auf dem Lande, manufakturkapitalistischer und industrieller Entwicklung betrachtet. Schließlich galt ein abschließender Gedanke der Förderung der gesellschaftlichen Entwicklung durch den Aufbau einer effektiven und zugleich maßvollen Verwaltungsorganisation, die in einigen Phasen der deutschen Geschichte beispielgebend für andere deutsche Territorialstaaten wurde.

Aus der sächsischen Geschichte ist das Besinnen auf die eigenen Möglichkeiten, das maßvolle Nutzen der Ressourcen des Landes für die eigene Bevölkerung und deren Bedürfnisse, der verantwortungsvolle Umgang mit der natürlichen Umwelt, dem Nachgehen als notwendig erkannter Maßnahmen mit der Schaffung weitschauender Lösungen auch unter schwierigen wirtschaftlichen Bedingungen und darin beruhender Schöpferkraft und Einfallsreichtum immer wieder neu zu lernen.

 

Vortrag am 9.2.1990
Bernd Wilhelmi (Jena), Ordentliches Mitglied der Mathematisch-naturwissenschaftlichen Klasse:

„Lichtmikroskopie. Ernst Abbe und sein Einfluß auf moderne Entwicklungen“

Am 23. Januar 1990 jährte sich der Geburtstag Ernst Abbes, Vater der modernen Lichtmikroskopie, Begründer des optischen Präzisionsgerätebaus, Mitglied der Sächsischen Akademie der Wissenschaften zu Leipzig, zum 150. Mal.

Aus diesem Anlaß betrachten wir die bisherige Geschichte der Lichtmikroskopie einschließlich moderner, zukunftsträchtiger Entwicklungen sowie den Einfluß dieses großen Gelehrten und erfolgreichen Unternehmers auf Theorie und Praxis der Optik, wobei zu bemerken ist, daß das Lichtmikroskop seit der Zeit Galileis beim Eindringen des Menschen in die Welt des Kleinen auf nahezu allen naturwissenschaftlichen Gebieten sowie in der Technik eine herausragende und andere Entwicklungen der Mikrodiagnostik befruchtende Rolle spielte und spielt.

Auf dem Weg vom Laboratorium eines Galilei, Janssen, Leeuvenhoek und Hooke zur modernen Meßtechnik ist Ernst Abbe (23.01.1840–14.01.1905) gemeinsam mit Carl Zeiß (11.09.1816–03.12.1888) wichtige Schritte gegangen. Ziel war es, wie F. Auerbach sehr klar beschreibt, „von den Grundgesetzen der Optik ausgehend, den Gang der Lichtstrahlen durch die Linsen und Zwischenräume hindurch in allen Einzelheiten wissenschaftlich verfolgen und daraufhin zu ehernen Formeln zu gelangen suchen, aus denen mit ma­thematischer Gewißheit zu entnehmen wäre, welche Durchmesser, Dicken, Krümmungen und gegenseitigen Abstände man Linsen geben müsse, um alle Fehler der Abbildung zu beseitigen oder, da dies doch wohl nicht zu erreichen sein würde, wenigstens auf ein Mindestmaß herabzudrücken. Kam dann noch eine ebenso exakte technische Ausführung hinzu, so konnte man sicher sein, mit dem fertigen Instrument keine Enttäuschung zu erleben.“

Bei der Lösung der komplizierten Gesamtaufgabe entwickelte sich Ernst Abbe zum Spezialisten auf mehreren naturwissenschaftlichen und technischen Gebieten, und er wurde zum Generalisten, der alle einzelnen Bemühungen dem großen Ziel unterordnete, leistungs­fähige optische Instrumente zu entwickeln, billig herzustellen und breit gefächerte Anwen­dungen zu erschließen.

Im Vortrag werden uns besonders wichtig erscheinende Beiträge Ernst Abbes zur Optik und zum optischen Präzisionsgerätebau untersucht, wobei wir in der Abfolge dem inhaltlichen Zusammenhang vor der Chronologie den Vorzug geben. Nach einer Einführung werden zunächst die Beiträge Ernst Abbes zur optischen Meß- und Prüftechnik sowie zur Technologie des optischen Instrumentenbaus diskutiert, was sowohl chronologisch als auch logisch begründet ist. Der Einstieg Ernst Abbes in die meßtechnischen und technologischen Aufgaben der optischen Werkstatt eröffnete ihm in besonderer Weise den Blick für alle ungelösten Probleme und für das Gesamtziel, förderte seine Entwicklung zum Generalisten. Darüber hinaus waren mehrere seiner Überlegungen, u.a. zur Längenmeßtechnik und Refraktometrie, so grundsätzlich und weitreichend, daß sie noch heute Grundlage aller Entwicklungen sind. Mit den neuen Meßgeräten erzielte Ernst Abbe in der Zeißschen Werkstatt zwei Effekte: Zum einen wurde die Übereinstimmung zwischen Konstruktion und nachfolgender Realisierung des optischen Instruments wesentlich ver­bessert, was den Beginn eines Präzisionsgerätebaus ermöglichte. Zum anderen konnte auf der Grundlage genauer Meß- und Prüfmöglichkeiten auch bei höchsten Anforderungen zur Fertigung von austauschbaren Teilen übergegangen werden, was eine weitgehende Arbeitsteilung und in der Folge eine große Produktivitätserhöhung im Mikroskopbau und später in anderen Zweigen des wissenschaftlichen Instrumentenbaus ermöglichte.

Im weiteren wird die Bedeutung der Abbeschen Arbeiten zur geometrischen und Wellenoptik und insbesondere zur Beugungstheorie der mikroskopischen Abbildung diskutiert. Mit großer Schärfe arbeitete Ernst Abbe den Zusammenhang zwischen ma­thematischen Abbildungen und deren optischer Realisierung heraus, fand dabei u.a. die Bedingungen für eine aberrations- und komafreie Abbildung mit weiten Bündeln und formulierte die Sinusbedingung. Bald zeigten ihm seine Experimente in der optischen Werkstatt, daß der Versuch, alle Bedingungen der geometrischen Optik für eine Minimierung der Abbildungsfehler einzuhalten nicht nur keine Verbesserung sondern erhebliche Ver­schlechterungen brachte. Die Frage „Worauf beruht es, daß ein großer Öffnungsfehler vollkommenere Bilder und feinere Details liefert als ein kleiner?“ führte Ernst Abbe zur Beugungstheorie des Mikroskops und damit zu einem qualitativ neuen Verständnis jeglicher optischer Abbildung, u.a. zur Formulierung eines beugungsbegrenzten Auflösungsver­mögens. Nachdem diese Grundlagen geschaffen waren, konnte Ernst Abbe in kurzer Zeit Mikroskope mit bis dahin unbekanntem Leistungsvermögen berechnen und in der Werkstatt bauen lassen. Die theoretischen Beiträge Abbes waren so fundamental, daß sie bis heute immer wieder zum Ausgangspunkt neuer Konzepte und Entwicklungen wurden, u.a. für das Zernikesche Phasenkontrastverfahren, für die Elektronenmikroskopie und für die Holographie.

Um alle errechneten Optiken mit guter Korrektion der Abbildungsfehler in weiten Wellenlängenbereichen verwirklichen zu können, benötigte man neue optische Materialien. Mit der ihm eigenen Gründlichkeit berechnete Ernst Abbe die erforderlichen Zusammen­hänge zwischen Brechzahl und Dispersion der „Wunschmaterialien“ und formulierte Anforderungen an Parametertoleranzen und Homogenität der optischen Werkstoffe. Empirisch fand er dabei Zusammenhänge zwischen Teildispersion und mittlerer Dispersion, die eine Folge der (damals noch unentdeckten) fundamentalen Kramers-Kronig-Relationen sind. Nach erfolgreichen Versuchen mit Flüssigkeitslinsen, die sich für eine praktische Nutzung kaum eigneten, beschritt Abbe zwei Wege. Zum einen führte er den Flußspat in die Objektivherstellung ein, wobei er selbst Lagerstätten erkundete und untersuchte. (Es sei bemerkt, daß Flußspat noch heute wegen seiner günstigen dispersiven Eigenschaften erfolgreich in Hochleistungssystemen verwendet wird). Zum anderen holte Abbe den jungen Glaschemiker Otto Schott nach Jena und entwickelte und erprobte gemeinsam mit ihm völlig neue Gläser, die den optischen Instrumentenbau infolge ihrer günstigen dispersiven Eigenschaften nachhaltig beeinflußten. Darüber hinaus gelang es, durch Anwendung präziser Meßverfahren und durch Optimierung der technologischen Prozesse die Reprodu­zierbarkeit der Parameter zu erhöhen sowie Homogenität, Transmission und Schlieren­freiheit zu verbessern. Die Arbeiten von Schott und Abbe wurden seither zum Ausgangs­punkt für die gezielte Entwicklung optischer Materialien.

Ein abschließender Abschnitt wendet sich neuen Wegen zur Erhöhung der räumlichen Auflösung zu. Ernst Abbe hatte mit seinen Arbeiten zunächst den Weg zur Ausschöpfung aller Möglichkeiten des Lichtmikroskops gewiesen und war selbst diesen Weg ein großes Stück vorausgegangen. Als universeller Denker ließ er sich durch die von ihm entdeckte Grenze für das räumliche Auflösungsvermögen nicht zu der Meinung verleiten, an einer prinzipiellen Grenze menschlicher Erkenntnis angekommen zu sein.

Mit seiner Theorie für das Auflösungsvermögen des Mikroskops, die nur auf die Wellennatur der Strahlung aber nicht auf spezielle Eigenschaften des Lichtes und schon gar nicht des sichtbaren Lichtes Bezug nimmt, hatte Ernst Abbe bereits Wege zur Beobachtung immer kleinerer Strukturen gewiesen. Leistungsfähige Mikroskope für ul­traviolettes Licht und in neuester Zeit für Röntgen-Strahlung sowie vielfältige Elektronen- ­und Ionenmikroskope bestätigten die Abbeschen Grundgedanken in glänzender Weise. Schließlich wurde in den letzten Jahren mit dem Nahfeldmikroskop, das alternativ als optisches Stethoskop bezeichnet wird, eine völlig neue Entwicklung eingeleitet, die es gestattet, mit sichtbarem Licht Auflösungen jenseits der Abbeschen Beugungsgrenze zu erreichen. Eine genaue Betrachtung zeigt, daß man auch diesen Gerätetyp ausgehend von den Abbeschen Grundgedanken behandeln kann, wobei man allerdings die Beschränkung auf eine Abbildung mit fortlaufenden freien Wellen fallen lassen muß.

Wenn abschließend nochmals nach der Auflösungsgrenze eines Lichtmikroskops gefragt wird, so könnte man aus gegenwärtiger Sicht antworten, daß diese durch die Dimensionen der kleinsten Antennen für diese Strahlung gegeben ist, und das sind die Atome selbst. Für die Geräte, mit denen man diese Grenze erreichen kann, wird ebenso wie für die Röntgen- und Elektronenmikroskopie die Aussage Abbes gelten, daß sie die Mikroskope seiner Epoche an Leistung weit übertreffen, aber mit ihnen nicht viel mehr als den Namen gemeinsam haben.

 

Vortrag am 9.2.1990
Heinz Schuster-Šewc (Leipzig), Ordentliches Mitglied der Philologisch-historischen Klasse:

„Das Sorbische und der Stand seiner Entwick­lung“

Verf. skizziert einleitend die sprachliche Stellung des Sorbischen im Rahmen der westslawischen Sprachen und verweist darauf, daß das heutige auf die Ober- und Niederlausitz beschränkte Wohngebiet nur einen Bruchteil des sich ursprünglich fast auf den gesamten Südteil der ehemaligen DDR erstreckenden altsorbischen Siedlungsgebietes darstellt. Es wurde im 12.–15. Jahrhundert eingedeutscht. Besprochen und etymologisiert wird weiter der ethnische Name Sorbe/Serb und sein Verhältnis zu der im Deutschen verwendeten Bezeichnung Wenden/Winden. Die Zahl der sorbisch (ober- und nieder­sorbisch) sprechenden Bevölkerung betrug Ausgang des vergangenen Jahrhunderts noch ca. 150 000 Personen, gegenwärtig kaum mehr als 50 000. Das Sorbische stellt sprachlich keine Einheit dar, es zerfällt in zwei dialektale Kerngebiete, das Ober- und Niedersorbische, repräsentiert seit dem 16./17. Jahrhundert durch zwei selbständige schriftsprachliche Formen, von denen die Obersorbische Schriftsprache im 19. Jahrhundert zu einem modernen, die Bedürfnisse von Publizistik, Literatur und Wissenschaft voll befriedigenden Gebilde entwickelt werden konnte. Es werden die sprachhistorischen und soziolinguistischen Gründe für die sprachliche Dualität des Sorbischen dargestellt. Verf. verweist auf die besondere Bedeutung des 19. Jahrhunderts für den nationalen und sprachlichen Aufschwung bei den Sorben (Gründung des wissenschaftlichen Bildungsvereins Maćica Serbska, Herausbildung der modernen obersorbischen Schriftsprache, Beginn der wissenschaftlichen Beschreibung des Sorbischen), in diesem Zusammenhang auch auf den Einfluß des tschechischen national-sprachlichen Entwicklungsmodells.

Mit der Übernahme des ersten slawistischen Lehrstuhls in Leipzig durch August Leskien entstehen neue Möglichkeiten für die wissenschaftliche Beschreibung des Sorbischen. 1891 veröffentlichte der Sorbe Arnošt Muka (ein Leskien-Schüler) das fundamentale Werk „Historische und vergleichende Laut- und Formenlehre der niedersorbischen (niederlausitzisch-wendischen) Sprache unter besonderer Berücksichtigung der Grenzdialekte und des Obersorbischen“, 1905 schließt er das Manuskript seines dreibändigen „Wörterbuches der niedersorbischen Sprache und ihrer Dialekte“ ab (erschienen 1915, 1926, 1928). Ein wichtiger Meilenstein in der Erforschung des Sorbischen ist die durch den russischen Linguisten L. V. Ščerba verfaßte und 1915 in Petrograd erschienene Monographie des Muskauer ostnieder­sorbischen Dialekts („Vostočnolužickoe narečie“). Diese Arbeit war zugleich ein wichtiger Beitrag zur Entwicklung der modernen sprachwissenschaftlichen Theorie (Präzisierung des von J. Baudouin de Courtenay vorgeschlagenen Phonembegriffs). In den zwanziger Jahren des 19. Jahrhunderts erschienen zwei große lexikalische Kompedien: 1. 1920 das „Deutsch-wendische (obersorbische) encyklopädische Wörterbuch“ von F. Rězak und 2. 1927 das „Wendisch-deutsche Wörterbuch der oberlausitzer Sprache“ von J. Kral. Zu entwickeln beginnt sich jetzt auch eine eigene sorbische Dialektologie, initiiert durch den Vasmer-Schüler Paul Wirth, der 1933 (Bd. 1) und 1936 (Bd. 2) seine „Beiträge zum sorbischen (wendischen) Sprachatlas“ veröffentlicht. Sie stellen qualitativ eine neue Stufe in der Erforschung des Sorbischen dar. Etwa zur selben Zeit beschäftigt man sich auch in Polen und in der Tschechoslowakei intensiv mit dem Sorbischen (W. Taszycki, Stieber, J. Pata).

Ein neuer verheißungsvoller Abschnitt der wissenschaftlichen Beschreibung des Sorbi­schen setzt nach 1945 ein. Wichtige Voraussetzung dafür war die 1951 erfolgte Gründung des Instituts für sorbische Volksforschung der Deutschen Akademie der Wissenschaften und des Sorbischen Instituts an der Leipziger Universität. Beide wissenschaftlichen Institutionen ermöglichten erstmals die Institutionalisierung der sorabistischen Forschung. Das Ergebnis sind zahlreiche wissenschaftliche Monographien und Buchpublikationen. Zu nennen sind vor allem die ersten deskriptiven Grammatiken (in sorbischer und deutscher Sprache), der Sorbische Dialektatlas (bisher 12 Bände), das Historisch-etymologische Wörterbuch der ober- und niedersorbischen Sprache (A–Ž/Ź, 24 Lieferungen) und die Edition der wichtigsten sorbischen Sprachdenkmäler. Breiten Raum nimmt in dieser Zeit auch die teilweise kontrovers geführte Diskussion über den sprachlichen Status des Sorbischen und das gegenseitige Verhältnis beider sorbischer Sprachzweige (eine oder zwei Sprachen) ein.

 

Vortrag am 12.1.1990
Uwe-Frithjof Haustein (Leipzig), Ordentliches Mitglied der Mathematisch-naturwissenschaftlichen Klasse:

„Die progressive Sklerodermie – Modell einer immunolo­gisch dysregulierten Fibrose“

In der Pathogenese der progressiven Sklerodermie spielen sich Veränderungen am Gefäßsystem ab (Wandfibrose, Devaskularisation), die vermutlich durch eine immunolo­gisch über Mediatoren ausgelöste Aktivierung der Fibroblastenfunktion verursacht werden. Die hier aufgezeigten Vorgänge werden durch genetische Faktoren mit bestimmt. Er­höhungen der Immunkomplexe, β-Galaktosidaseaktivität und des N-Prokollagenpeptides im Serum sowie der Hexuronsäureausscheidung im Urin korrelieren mehr oder weniger gut mit der Aktivität und Ausdehnung der Erkrankung (Manifestation innerer Organe wie Gastrointestinaltrakt, Lunge, Herz und Niere). Die Bestimmung von Antikörpern gegen verschiedene Kernbestandteile (ANF, Anticentromer-, Antitopoisomerase-Antikörper) helfen bei der Einordnung der Krankheit hinsichtlich ihrer Subsets und Prognose.

Durch die Isolierung der ribosomalen RNA aus Hautbiopsien gelang in vivo mit gentechnologischen Methoden im Northern- und Dot-Blot der Nachweis, daß die mRNA nur für Kollagen Typ I, nicht aber für Kollagen Typ III, Kollagenase und Fibronektin erhöht ist. Diese selektive Hochregulation von Kollagen Typ I mRNA ist als Beweis der gesteigerten Synthese durch Fibroblasten anzusehen. In Monolayer-Fibroblastenkulturen wurde der differenzierte Einfluß verschiedener Zytokine (TGFβ, IL-l, IFNγ) auf den Fibroblasten untersucht und gezeigt, daß der Fibroblast einer immunologischen Regulation unterliegt, die wahrscheinlich bei der PS gestört ist (immunologisch dysregulierte Fibrose). Schließlich scheint im Siliziumdioxid als der einzigen von zahlreichen Umweltsubstanzen mit PS nachahmendem Effekt ein ätiologisch gesicherter Trigger der PS-Pathogenese gefunden zu sein. Auf Grund epidemiologischer, klinischer, immunologischer Daten, Marker des Fibroblastenstoffwechsels und der Endothelzellfunktion wurde bewiesen, daß die nach Langzeitsiliziumdioxidexposition mit Silikose assoziierte PS mit der idiopathischen PS identisch und als Berufskrankheit anzuerkennen ist.

Die Therapie ist auf die Verbesserung der Durchblutung (Dextran, Corinfar^R, Ralofect^R), Hemmung entzündlicher Prozesse (Prednisolon, Azathioprin) und die Beeinflussung des Bindegewebsstoffwechsels (Penicillin, Penicillamin) ausgerichtet. Physiotherapeutische Maßnahmen und psychische Führung sind die unerläßliche Basis jeglicher Behandlung.

 

Vortrag am 12.1.1990
Peter Nagel (Halle-Wittenberg), Ordentliches Mitglied der Philologisch-historischen Klasse:

„Die Septuaginta als Ziel und Ausgangspunkt antiker Übersetzungsliteratur“

Die uns geläufige Bezeichnung „Septuaginta“ für die griechische Übersetzung des hebräischen (in einigen Passagen aramäischen) Alten Testaments kam als Buchtitel erst seit Augustinus (de civitate Dei 18,42) in Gebrauch. Sie geht zurück auf die „septuaginta interpretes“ (genauer: 72 Übersetzer), die dem Aristeasbrief zufolge die Übersetzung der hebräischen Thora ins Griechische in 72 Tagen vollendeten. Durch Philo von Alexandria (Leben des Mose 2,25–44) wird die Erzählung des Ps.-Aristeas um drei folgenreiche Motive erweitert:

1. Die Übersetzung erstreckt sich auf das gesamte Alte Testament;
2. sie stimmt bei allen 72 Übersetzern, obwohl sie voneinander getrennt in Klausur arbeiteten, wortwört­lich überein;
3. die Übersetzung der „septuaginta“ ist inspiriert und hat die gleiche Dignität und Autorität wie das hebräische Original.

Den legendären Berichten über den Ursprung der Septuaginta, deren Hauptmotiv in der Autorisierung des griechischen Bibeltextes, wie er unter den griechischsprachigen Juden Alexandrias und der Diaspora insgesamt in Gebrauch war, liegt, wird die Übersetzungstheo­rie und -praxis des Altertums unter drei Gesichtspunkten gegenübergestellt:

1. die Frage nach der Übersetzbarkeit von Texten, speziell von heiligen Schriften;
2. der Übersetzungs­modus, nämlich verbum de verbo (wörtlich) oder sensus de sensu (sinngemäß), d.h. die Frage der Adäquatheit einer Übersetzung gegenüber der Ausgangssprache;
3. die Vielfalt der Textzeugen, die das Problem der Rezensionen und des Archetypus aufwerfen.

Die Wege und Wertung der Septuaginta sind in Judentum und Christentum völlig gegensätzlich. Das Judentum zieht sich unter Verwerfung der Septuaginta auf Text und Umfang (Kanon) des hebräischen Originals zurück, während für das Christentum die Septuaginta noch vor dem Neuen Testament die heilige Schrift schlechthin darstellt und insbesondere dem christologischen Weissagungsbeweis dienstbar gemacht wird – wobei der abweichende Wortlaut zwischen dem hebräischen und griechischen Text zum Anlaß erbitterter Polemik wird.

Der ursprünglich jüdischen, in der Sicht des rabbinischen Judentums diskreditierten, weil von den Christen usurpiert und korrumpiert, Septuaginta werden neue jüdisch-griechische Übersetzungen entgegengestellt, die mit den Namen von Aquila, Symmachus und Theodo­tion verbunden sind. Sie sind bis auf geringe Reste untergegangen, weil sie innerhalb des Judentums nicht als heilige Schriften galten (nur die Lesung des Aquila war im Synagogen­gottesdienst erlaubt).

Die Vielfalt der Septuagintalesarten gab Anlaß zur Sammlung, Sichtung und Rezension der umlaufenden Texte, die in der von Hieronymus beklagten trifaria varietas des Septuagintatextes (Origenes/Euseb, Lukian und Hesych) ihren Niederschlag fand. Die textgeschichtliche Erforschung der Septuaginta ist bemüht, die Geschichte (und Vorstufen) der Rezensionen aufzuhalten mit dem methodischen Prinzip und Ziel, die Textgestalt der Septuaginta vor den greifbaren Rezensionen herzustellen.

Der Archetyp der Septuaginta ist schwer faßbar, da nichtrezensierte Texte (darunter jüdische Septuagintapapyri) nur sehr spärlich belegt sind. Als Haupttendenz ist eine fortwährende Überarbeitung und Angleichung an den hebräischen Wortlaut erkennbar, der seinerseits während der Entstehungszeit der Septuaginta noch nicht standardisiert war. Die Targumhypothese Paul Kahles über den Ursprung der Septuaginta, die die Suche nach dem Archetyp methodisch ausschließt, ist ebenso einseitig wie die Annahme einer schriftlichen Urfassung. Sehr wahrscheinlich ist der Ursprung in der mündlichen Über­setzung im Gottesdienst, bei der sich eine feste Übersetzungspraxis herausbildete, die seit dem 3. Jh. v. Chr. allmählich schriftlich fixiert wurde (Fr. Rehkopf).

Die Septuaginta, ursprünglich das Ergebnis eines Übersetzungsprozesses, wurde im Schoße des Christentums zum Ausgangspunkt neuer nationalsprachlicher Versionen, von denen sich das Armenische und das Koptische erst im Zuge der Bibelübersetzung zu Schriftsprachen herausbildeten. Diese Übersetzungen sind Zeugnis für den Übergang der kirchlichen Mission von der Weltsprache Griechisch zu „Randsprachen“ und für die Herausbildung neuer nationaler Schriftsprachen und Nationalkirchen. Ein eigentümlicher Unterschied macht sich bei der Übersetzungsgeschichte des Alten Testaments auf den Boden bereits ausgebildeter Schriftsprachen geltend. Im Bereich des Lateinischen wurde die auf der Septuaginta basierende altlateinische Version durch die aus dem Hebräischen übersetzte Vulgata verdrängt; die kirchlich rezipierte syrische Übersetzung (Peschitta) hat den hebräischen Text zur Grundlage, während erst spätere (gelehrte, nicht dem gottesdienst­lichen Gebrauch dienende) Übersetzungen auf die Septuaginta zurückgriffen. Bevor die Tochterversionen der Septuaginta für die Textgeschichte und Textkritik der Sep­tuaginta selbst nutzbar gemacht werden können, gilt es ihre eigene Textgeschichte zu erhellen und das linguistische Verhältnis zwischen den Sprachen der Septuaginta und ihren Tochterversionen zu erforschen. Beide Aufgaben stehen noch ganz in den Anfängen.